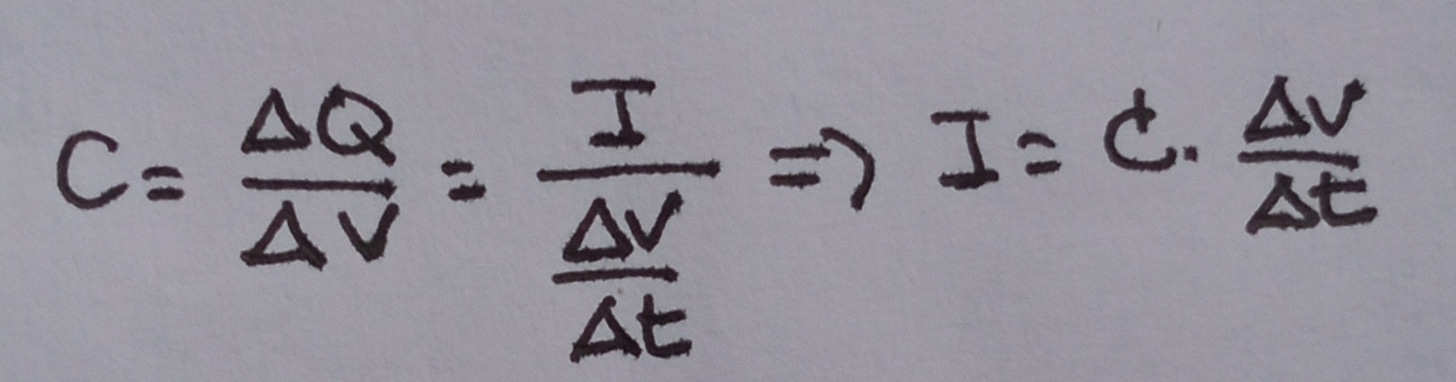Signal Integrity fundamentals
High speed digital design is not black magic, but engineering magic
Problem statement
Consider the most basic circuit: a battery, a switch and a resistor.
When the switch is open, no current flows through the circuit, but when you close it, the current is established by Ohms law.
Now, imagine that we need to place the resistor over the Moon's surface at 400.000 km away. Imagine also that for this purpose we use a large stock of a well known coaxial cable: RG58. To propagate over the cable, the signal takes about 2 seconds, one 1.5 times more time than light takes to propagates over vacuum.
When the switch is open, the behavior is the same we had before: no current flows.
Life is change
However, when the close the switch, we find something astonishing: the battery does not know which current has to provide as the signal needs nearly 2 s to reach the load and another 2 other seconds to return the information.
What happens can be easily understood if we mentally divide the cable in small pieces, for example one meter segments.
If we have a look to the datasheet, se see that the signal needs 5 ns to propagate through one meter. In this time, it needs a current to charge the cable capacity of the section, which is 100 pF for one meter.
How much current do you need to charge 100 pF in 5 ns?
The current you need to apply is the same you need to drive a 50 Ω load! This is the cable characteristic impedance. It is a very important parameter of the cable that is highlighted in the cable datasheet.
After 5 ns this first section is already charged, the step has propagated 1 m, but now, is the next 1 m section the one that needs to be charged and for this, more current has to be provided and so on.
During the two seconds that the signal needs to reach the moon, the battery will be providing a constant current to charge the cable to its voltage.
During the step propagation, the battery does not see the load, sees only the cable, which behaves as a resistor, a 50 Ω resistor.
The signal reaches destination
When the signal reaches the end, about two seconds after switch closure, every section of the cable is charged. The cable alone requires no more current.
The step arrives to the termination resistor, the Ohm’s Law applies again. The resistor current is set as in the first figure: I=V/R.
It the load impedance is a resistor with the same value of the cable characteristic impedance (50 Ω) the same amount of current that was flowing across the cable is the one the load needs. If it where so, the battery current would not change at all, no discontinuity is seen. The system has reached steady state.
Now, it comes an interesting thing: if the load impedance where not a 50 Ω resistor, the current that the resistor needs is different than the one has has been flowing across the cable and in order to fulfill the Kirchhoff laws, part of the current will be reflected back to the source.
Summary and conclusions
The conclusions are the following:
In a High Speed design, we will see different waveforms in different line places.
When the pulse starts, the generator sees only the cable, not the load. Current is determined by the ratio of voltage to cable characteristic impedance.
If the load impedance is equal to the cable characteristic impedance we say that the cable is properly terminated. There is no pulse distortion at the end. No signal is reflected back.
If the load impedance is different to the cable characteristic impedance, the received pulse changes and reflects back to the source.
Not proper termination may take place in the destination, in the source or in intermediate points. In any point in which there is a discontinuity, there will be signal reflection.
In the next newsletter post we will leave Moon wiring activities and we will move into more terrestrial electronics, but we will be able to see that the real challenges that the digital engineer has to face are very close to the ones we have introduced today, because modern electronics are extremely fast.